Ejemplo tomado de (wikipedia)
Ejemplos
- La función definida por
 , tiene como dominio, codominio e imagen a todos los números reales
, tiene como dominio, codominio e imagen a todos los números reales 
- Para la función
 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
, sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
- En la figura se puede apreciar una función
 , con
, con
- Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,
- Esta función representada como relación, queda:
 .
. - En este ejemplo podemos ver dos conjuntos el (X) y el (Y), el cual se une y forma las parejas ordenadas y esta rodena por el método de mayor que. Si miramos la gráfica nos muestra como se ordenan las parejas ordenadas con flechas que van desde el grupo (X) al grupo (Y). Formando la función real.


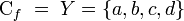

No hay comentarios:
Publicar un comentario